1. 什么是分治算法
在计算机科学中,分治法是建基于多项分支递归的一种很重要的算法范式。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
这个技巧是很多高效算法的基础,如排序算法(快速排序、归并排序)、傅立叶变换(快速傅立叶变换)。
另一方面,理解及设计分治法算法的能力需要一定时间去掌握。正如以归纳法去证明一个理论,为了使递归能够推行,很多时候需要用一个较为概括或复杂的问题去取代原有问题。而且并没有一个系统性的方法去适当地概括问题。
分治法这个名称有时亦会用于将问题简化为只有一个细问题的算法,例如用于在已排序的列中寻找其中一项的折半搜索算法(或是在数值分析中类似的勘根算法)。这些算法比一般的分治算法更能有效地执行。其中,假如算法使用尾部递归的话,便能转换成简单的回圈。但在这广义之下,所有使用递归或回圈的算法均被视作“分治算法”。因此,有些作者考虑“分治法”这个名称应只用于每个有最少两个子问题的算法。而只有一个子问题的曾被建议使用减治法这个名称。
分治算法通常以数学归纳法来验证。而它的计算成本则多数以解递回关系式来判定。
来源:https://zh.wikipedia.org/zh-hans/分治算法
2. 分治策略
对于一个规模为n的问题,如果该问题可以分解成k个较小的、相似的子问题,并且这些子问题之间相互独立,并且与原问题形式相同,那么可以递归这些子问题,最后将这些子问题合并,得到最终解。分治经常是与递归一起使用解决问题。
3. 适用情况
分治算法能够解决的问题一般有如下特征:
- 该问题分割缩小到一定程度就可以很容易解决。
- 该问题可以分解成k个相同的子问题。
- 各个子问题是相互独立的。
- 分解出的所有子问题的解能够合并成最终的大问题的解。
4. 基本步骤
分治算法在每一层的递归上,都有如下的3个步骤
- 分解:将原问题分解成若干个规模较小的子问题,并且子问题相互独立,与原问题形式相同。
- 解决:若子问题规模较小,并且很容易解决问题,那么直接解决问题,否则递归继续分解。
- 合并:将子问题的解合并成原问题的解。
5. 可以解决的经典问题
- 二分搜索
- 大整数乘法
- Strassen矩阵乘法
- 归并排序
- 快速排序
- 棋盘覆盖
- 汉诺塔
- 循环赛日程表
- 最接近点对问题
6.实例
6.1 二分搜索
问题:给定一组有序的数组[1,2,3,4,5,6,7,8,9,10],较快的从中选择出9,并返回其下标。
分治说明:
- 分解:将数组拆分成2份,然后将中位值下标 k=5 的值与 9 做比较,等于则直接返回,否则获取大于 9 的那一段,重复分解,直到分解到最后一个。
- 解决:分解到最后一个数组的时候,判断是否找到。
- 合并:将结果直接返回。
画图解析

算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
* @author sk
* @date 2021/3/01
* @description 二分搜索
*/
public class BinarySearch {
public static int search(int[] num, int left, int right, int find) {
if (left > right) {
//边界条件,没找到
return -1;
}
//中位值
int mid = (left + right) / 2;
int m = num[mid];
if (m == find) {
//直接找到,返回
return mid;
} else if (m > find) {
//分治递归
//需要查找的值大于中位值num[mid]
return search(num, left, mid - 1, find);
} else {
//分治递归
//需要查找的值小于中位值num[mid]
return search(num, mid + 1, right, find);
}
}
public static void main(String[] args) {
int[] num = new int[10];
for (int i = 0; i < 10; i++) {
num[i] = i;
}
int find = 8;
int result = search(num, 0, num.length - 1, find);
System.out.printf("搜索:[%s],下标:[%s]", find, result);
}
}
6.2 归并排序
问题:将一组无序的数组num=[9,5,1,4,3,8,7,6,0,2]进行排序
分治说明:
- 分解:将数组num平均分成2段数组,然后这2段数组继续平均切割,直到数组切割成单个数字。
- 解决:将所有分解到最后的单个数字与相邻的数字进行排序合并。
- 合并:由下向上继续排序合并。
画图解析
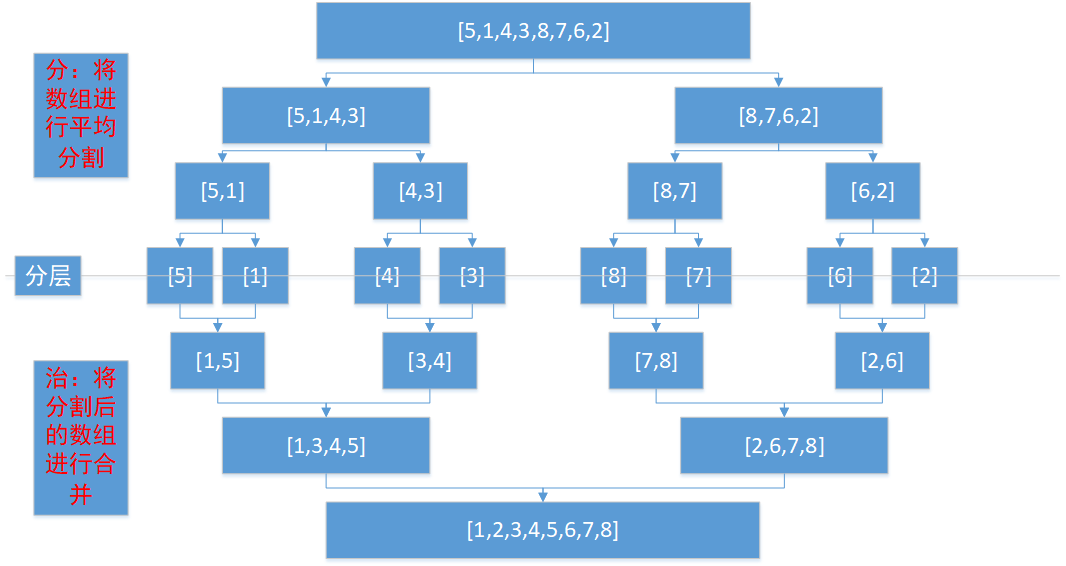
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import java.util.Arrays;
/**
* @author sk
* @date 2021/3/01
* @description 归并排序
*/
public class MergeSort {
public static void main(String[] args) {
int[] num = new int[]{9,5,1,4,3,8,7,6,0,2};
int[] temp = new int[num.length];
spit(num, 0, num.length - 1, temp);
System.out.println(Arrays.toString(num));
}
/**
* 切割
* @param num 原数组
* @param left 数组左端
* @param right 数组右端
* @param temp 暂存数组
*/
public static void spit(int[] num, int left, int right, int[] temp) {
if (left < right) {
//将数组平均分成2段
int mid = (left + right) / 2;
//再切割左端数组
spit(num, left, mid, temp);
//再切割右端数组
spit(num, mid + 1, right, temp);
//左右排序合并
merge(num, left, right, temp);
}
}
public static void merge(int[] num, int left, int right, int[] temp) {
int mid = (left + right) / 2;
int l = left;
int r = mid + 1;
int t = 0;
while (l <= mid && r <= right) {
if (num[l] >= num[r]) {
//左端数字 > 右端数字,则将右端数字放到temp里面
temp[t++] = num[r++];
} else {
//左端数字 < 右端数字,则将左端数字放到temp里面
temp[t++] = num[l++];
}
}
//如果左端还有剩余数字,证明剩余的数字都是比右端的大,故直接放入缓存数组
while (l <= mid) {
temp[t++] = num[l++];
}
//如果右端还有剩余数字,证明剩余的数字都是比左端的大,故直接放入缓存数组
while (r <= right) {
temp[t++] = num[r++];
}
t = 0;
//将缓存数组里面的数字替换到原数组中
while (left <= right) {
num[left++] = temp[t++];
}
}
}